Devlog 5: Organic Particle Motion With Cubic Bezier Curves

Last week I added click particles that burst out when you tap. They looked okay, but something felt off. The particles followed straight linear paths, which looked mechanical and boring.

I wanted particles to flow smoothly, following curved trajectories. Like they're being pulled by gravity toward the vote counter, not just flying in straight lines.

The solution: cubic Bezier curves. I had already used cubic Bezier easing for smooth vote counter animations, and the same mathematical technique works beautifully for particle trajectories.

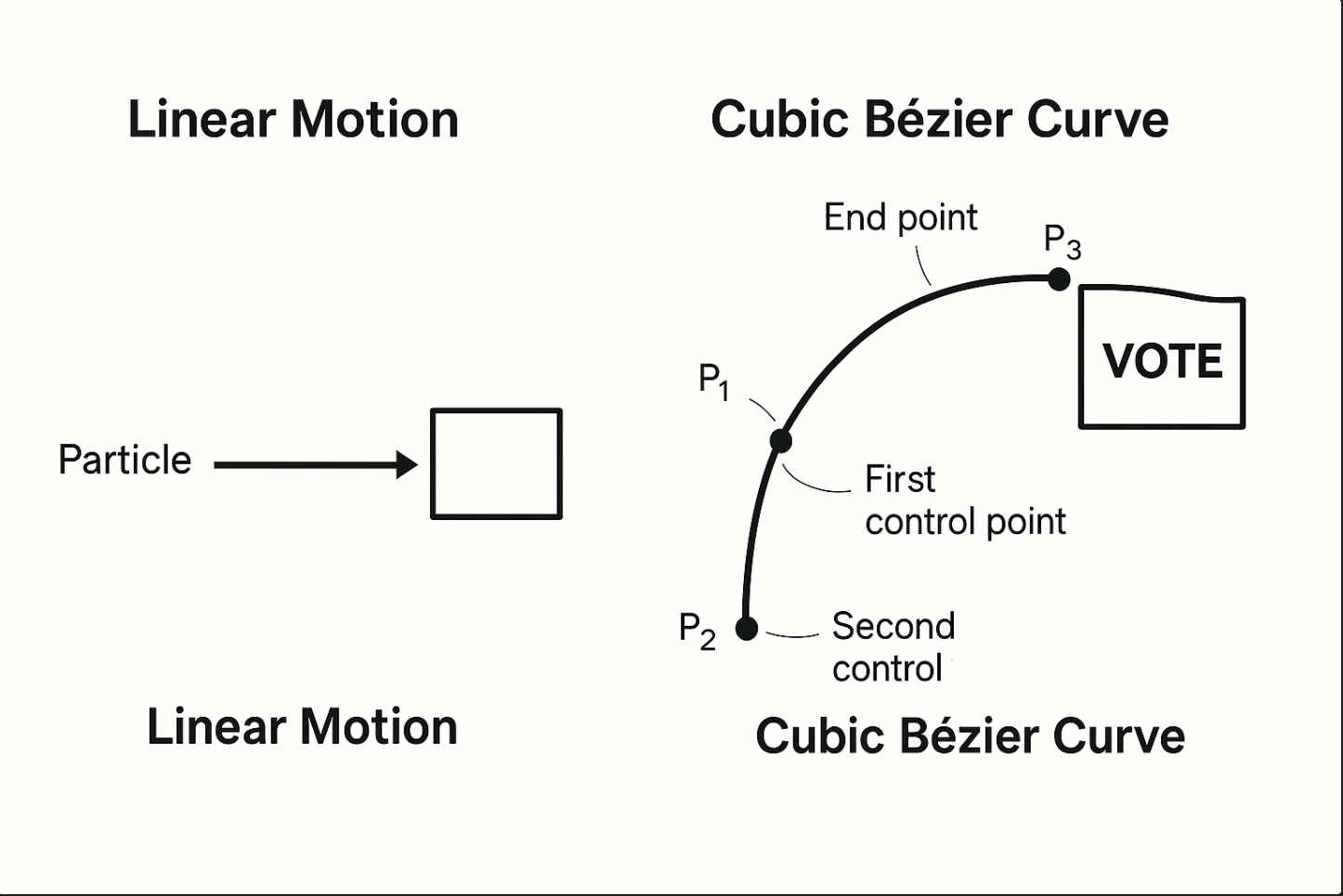
The Problem With Linear Motion

My first implementation had particles move in straight lines:

// Update each frame
particle.x += particle.velocityX * delta;
particle.y += particle.velocityY * delta;

This creates perfectly straight paths from the spawn point to wherever they disappear. Mathematically simple, visually boring.

Real-world motion is curved. Thrown objects arc through the air. Water flows along curves. Organic movement is rarely linear.

Bezier Curves for Animation Paths

A cubic Bezier curve is defined by 4 points:

• P0: Start point (where you clicked)
• P1: First control point (influences initial direction)
• P2: Second control point (influences end direction)
• P3: End point (where particle disappears)

The particle follows a smooth curve between P0 and P3, influenced by P1 and P2.

Here's how I implemented it:

interface Particle {
  // Bezier curve control points
  startX: number;
  startY: number;
  controlX1: number;
  controlY1: number;
  controlX2: number;
  controlY2: number;
  endX: number;
  endY: number;

  // Animation progress (0 to 1)
  progress: number;
  duration: number;
}

function spawnParticle(clickX: number, clickY: number, targetX: number, targetY: number) {
  const particle = getAvailableParticle();

  // Start where user clicked
  particle.startX = clickX;
  particle.startY = clickY;

  // First control point: shoot out radially
  const angle = Math.random() * Math.PI * 2;
  const distance = 50 + Math.random() * 50;
  particle.controlX1 = clickX + Math.cos(angle) * distance;
  particle.controlY1 = clickY + Math.sin(angle) * distance;

  // Second control point: curve toward target
  particle.controlX2 = targetX + (Math.random() - 0.5) * 100;
  particle.controlY2 = targetY - 50; // Bias upward

  // End at vote counter
  particle.endX = targetX;
  particle.endY = targetY;

  particle.progress = 0;
  particle.duration = 1.0 + Math.random() * 0.5; // 1-1.5 seconds
}

Each particle gets a unique curved path from the click point to the vote counter.

Evaluating the Bezier Curve

Every frame, I advance progress from 0 to 1 and calculate the particle's position along the curve:

function cubicBezier(t: number, p0: number, p1: number, p2: number, p3: number): number {
  const t2 = t * t;
  const t3 = t2 * t;
  const mt = 1 - t;
  const mt2 = mt * mt;
  const mt3 = mt2 * mt;

  return (mt3 * p0) +
         (3 * mt2 * t * p1) +
         (3 * mt * t2 * p2) +
         (t3 * p3);
}

function updateParticle(particle: Particle, delta: number) {
  particle.progress += delta / particle.duration;

  if (particle.progress >= 1) {
    // Particle reached end, return to pool
    particle.alpha = 0;
    return;
  }

  // Calculate position along curve
  particle.x = cubicBezier(
    particle.progress,
    particle.startX,
    particle.controlX1,
    particle.controlX2,
    particle.endX
  );

  particle.y = cubicBezier(
    particle.progress,
    particle.startY,
    particle.controlY1,
    particle.controlY2,
    particle.endY
  );

  // Fade in/out
  if (particle.progress < 0.1) {
    particle.alpha = particle.progress / 0.1; // Fade in
  } else if (particle.progress > 0.9) {
    particle.alpha = (1 - particle.progress) / 0.1; // Fade out
  } else {
    particle.alpha = 1;
  }
}

This creates smooth arcing motion from the click point to the vote counter.

Randomizing Control Points

If all particles followed the same curve, it would look repetitive. I randomize the control points:

• Control point 1: Shoot out in a random radial direction
• Control point 2: Near the target, but with some randomness
• Duration: Each particle takes 1-1.5 seconds (randomized)

This creates organic variation. Some particles take tight curves, others sweep in wide arcs. It looks natural and dynamic.

Performance Concerns

Bezier math has multiplications and polynomials. I was worried it might be too expensive for hundreds of particles at 60fps.

But testing showed it's fine:

• Modern CPUs handle this math easily
• Bezier evaluation is O(1) per particle
• Way cheaper than the WebGL rendering PixiJS does

I can run 200+ particles with Bezier curves at 60fps on a cheap phone. No problem. Later, I optimized the particle system further with PixiJS and object pooling to ensure consistent 60fps performance even on budget devices.

The Visual Difference

Before Bezier curves: Particles shoot out in straight lines and disappear. Looks like a simple burst effect.

After Bezier curves: Particles arc elegantly toward the vote counter, like they're being pulled in. Looks organic and satisfying.

It's such a subtle change, but the perceived quality jumps massively. The animation feels polished instead of cheap.

Alternative: Pre-Calculated Paths

An optimization I considered: pre-calculate the curve into an array of positions, then just index into it each frame. This would trade memory for CPU time.

I didn't bother because:

1. The math is already fast enough
2. Pre-calculating limits runtime variation
3. Memory usage would scale with particle count

Sometimes the "obvious" optimization isn't necessary. Measure first, optimize later.

Takeaway

Bezier curves are one of those tools I learned about in school but never actually used. Turns out they're perfect for animation paths.

The math looks intimidating but the implementation is straightforward. Don't let polynomial equations scare you away.

Organic motion requires randomness + curves. Linear motion is predictable. Curved motion with variation is alive.

This is another one of those details most users won't consciously notice. But it contributes to the overall feeling that Tuggy is polished and satisfying to use.

Particle systems are where game development and web development overlap. Turns out game dev techniques work great for making UIs feel good.